
COMUNICACIÓN SOLICITADA
MESA GUTIÉRREZ JC1, GARCÍA GARCÍA O2, ARRUGA GINEBREDA J3
Hospital Universitari Bellvitge. Barcelona.
1 Doctor en Medicina. Máster MBE Colaboración Cochrane. MIR
Oftalmología.
2 Licenciado en Medicina. Tutor de residentes. Médico adjunto.
3 Doctor en Medicina. Jefe de Servicio.
RESUMEN
La medicina basada en la evidencia (MBE) es el uso consciente y juicioso de la mejor evidencia disponible en la toma de decisiones. Se trata de actuar en la clínica utilizando información seleccionada y relevante, y que venga avalada por datos obtenidos a través del método científico más riguroso: la epidemiología y la estadística. La MBE resta fuerza a la intuición, la experiencia clínica no sistematizada y la fisiopatología como elementos suficientes para la toma de decisiones clínicas, y acentúa el valor del examen riguroso de las pruebas científicas suministradas por la investigación clínica.
La evaluación crítica de los artículos relacionados con las alternativas terapéuticas constituirá nuestro objetivo. Suministraremos las habilidades básicas para la evaluación y análisis de los artículos científicos mediante el uso de una serie de conocimientos sencillos de estadística, diseño de investigaciones y epidemiología clínica.
DEFINICIÓN Y ANTECEDENTES
La medicina basada en la evidencia (MBE) es el uso consciente, explícito y juicioso de la mejor evidencia disponible en la toma de decisiones sobre los cuidados de pacientes individuales (1). Este término fue acuñado en los años 80 por un grupo de internistas y epidemiólogos clínicos canadienses de la Universidad de McMaster, que más tarde formarían el Evidence-Based Medicine Working Group y su difusión en la práctica clínica se produjo a partir de 1992 con la serie de artículos publicados en la revista JAMA (2). Su sistemática de trabajo ha ido progresivamente arraigando en la comunidad médica, y el resultado se ha consolidado como un nuevo paradigma o «estilo del saber médico» (3) acerca de los conocimientos necesarios para orientar la práctica clínica.
La práctica médica tradicional, heredera de los paradigmas clásicos, pero vigente todavía hoy en muchos ámbitos, se puede caracterizar por la creencia en que:
a) Las observaciones derivadas de la experiencia clínica personal son una forma válida de generar, validar y transmitir los conocimientos acerca del pronóstico de las enfermedades, el rendimiento clínico de las pruebas diagnósticas y la eficacia o eficiencia de los tratamientos.
b) Un buen conocimiento de la teoría fisiopatológica subyacente, una combinación de habilidad en el razonamiento y la especulación lógica, y una buena dosis de sentido común permiten interpretar adecuadamente los signos de la enfermedad y elegir el tratamiento más adecuado; y
c) Los conocimientos se actualizan adecuadamente mediante libros de texto y revistas con los tradicionales «artículos de revisión», en los que los expertos de más experiencia y prestigio nos seducen con sus opiniones juiciosas acerca de las soluciones a los problemas clínicos. Es por ello que se concede una enorme credibilidad al argumento de autoridad, y los apartados «introducción» y «discusión» de los trabajos de investigación original centran los debates y marcan las pautas de actuación para una «buena praxis».
Sin embargo, la práctica clínica diaria nos sigue demostrando el error de las premisas anteriores y su insuficiencia para guiar nuestras decisiones cotidianas. Debemos aceptar que desconocemos el impacto real de muchas de las medidas que tomamos en nuestro quehacer cotidiano, pues su eficiencia clínica nos parece intrínseca a su coherencia con la base fisiopatológica teórica del problema. Un ejemplo claro de ello nos lo ha proporcionado el uso de la seroalbúmina en el tratamiento de pacientes hipoproteinémicos. Parece evidente que en pacientes gravemente hipoalbuminémicos tenga sentido fisiopatológico administrar albúmina intravenosa para restaurar la cifra de esta proteína plasmática y así mejorar el pronóstico del paciente evitando la formación de edemas. Pero una revisión sistemática de la literatura ha demostrado que en pacientes hipoproteinémicos (y también en quemados), el uso de albúmina para restaurar sus niveles plasmáticos no sólo no mejora el pronóstico, sino que produce mayor mortalidad (4). En concreto, hay que administrar albúmina a 16 pacientes hipoproteinémicos para producir una muerte. Si esto no es coherente con la hipotética base fisiopatológica, el método científico que hemos desarrollado desde el Renacimiento nos ha enseñado que probablemente lo erróneo sea la teoría que nuestra mente ha construido para explicar el problema. Con un experimento sencillo fue como, en el siglo XVI, Harvey demostró que las teorías de Galeno sobre la circulación inmutablemente vigentes desde el imperio romano eran falsas, inaugurando la «nueva práctica» de una medicina científica (5).
La historia del uso del suero frío en la hemorragia digestiva nos ilustra de lo endeble que resulta basar nuestra práctica clínica en el «argumento de autoridad». Esta medida terapéutica alcanzó una gran difusión una vez que fue planteada por Wangensteen a finales de los 50, a partir de sus trabajos experimentales con perros. A pesar de los deficientes resultados conseguidos en la clínica, de trabajos posteriores en los que se observaba un efecto perjudicial del frío sobre la mucosa del estómago y sobre la coagulación, y de que los resultados eran similares si se utilizaba agua corriente, los tratados clásicos de cirugía de los años 80 seguían planteando esta opción en el tratamiento empírico de la hemorragia digestiva alta (6). También el sistema tradicional de reciclaje de conocimientos, el famoso sistema de aprendizaje mediante sesiones de «Formación Médica Continuada», ha quedado obsoleto, puesto que los libros de texto tradicionales son incapaces de recoger la nueva información científica que se produce en tiempo real. Así, después de 43 ensayos clínicos aleatorizados (en los que participaron más de 21.000 pacientes) en que se demostraba la eficacia de la trombólisis temprana sobre la mortalidad del infarto de miocardio, ningún libro de texto médico establecía aún esta indicación como rutinaria. Pero aún hay más: al igual que en el caso del suero frío, en 1990 y después de 15 ensayos clínicos aleatorizados y tres metaanálisis, se seguía recomendando en los textos especializados la administración profiláctica de lidocaína para prevenir el re-infarto, un medida completamente ineficaz (7) .
Por otra parte, en las últimas décadas hemos asistido al fenómeno de la explosión informativa, un crecimiento exponencial de la literatura médica que hace materialmente imposible mantenerse al día si pretendemos hacerlo utilizando este recurso de una manera acrítica. En 1948 había cerca de 4.700 revistas científicas; en 1994 se publicaban unos 2 millones de artículos en 20.000 revistas médicas (8). Aunque quizá en nuestra especialidad sea más sencillo dado (por el momento) el menor volumen de información a consumir, se estimó que para mantenerse al día, un generalista debería leer 19 artículos al día durante los 365 días del año (9). Si combinamos este hecho con la mejora actual en el acceso a la información gracias internet, el resultado es una avalancha de información que obliga al médico que no quiera ir perdiendo competencia profesional con el paso del tiempo, a dominar habilidades y técnicas sistemáticas que le doten de sentido crítico y le permitan identificar la información verdaderamente relevante para su práctica «a pie de paciente». Necesitamos el imán que nos permita buscar la aguja en el pajar, puesto que con el actual ritmo de producción de ensayos clínicos y otras investigaciones rigurosas, la cuestión ha dejado de ser si nuestras actuaciones en la práctica tienen buena base científica, sino cuánta de la evidencia actualmente disponible se aplica en la práctica diaria (10).
Frente al modelo tradicional, la MBE se caracteriza por la creencia en que:
a) La información derivada de la experiencia clínica y la intuición puede llevar a conclusiones erróneas si no se basa sólidamente en observaciones sistemáticas.
b) El estudio y conocimiento de los mecanismos teóricos básicos de la enfermedad es necesario pero insuficiente para guiar la práctica clínica.
c) El profesional necesita conocer ciertas reglas para evaluar rigurosamente la metodología con la que se han obtenido las pruebas científicas en las que se sustentan sus decisiones.
La MBE resta fuerza a la intuición, la experiencia clínica no sistematizada y la fisiopatología como elementos suficientes para la toma de decisiones clínicas, y acentúa el valor del examen riguroso de las pruebas científicas suministradas por la investigación clínica. Para ello incorpora al arsenal de saberes y habilidades básicas para el desempeño de la profesión médica, la destreza en el uso de una serie de conocimientos sencillos de estadística, diseño de investigaciones y epidemiología clínica.
Los médicos deben, pues, adquirir la responsabilidad de evaluar de forma crítica e independiente la credibilidad tanto de las evidencias como de las opiniones ofertadas. Lo importante no es el mensaje, sino el método con el que se ha llegado a los datos. Para los científicos la validez del conocimiento teórico radica en si resiste la dura prueba que supone el experimento. No importa lo maravillosa, ingeniosa o coherente que nos parezca la conjetura que hemos supuesto, ni cómo se llama o qué cargo ocupa el que la formuló: si un experimento contradice a la teoría, la teoría es falsa (11). Son ahora los apartados «material y métodos» y «resultados» de los artículos de investigación los que se convierten en las piezas claves de los trabajos médicos, pues son las secciones que deben evaluarse detalladamente para valorar la validez de los datos que aporta. Así que para este nuevo estilo científico de hacer medicina, la autoridad establecida los «expertos», tienen mucho menor peso. Por eso Sackett (12), convertido a su vez en experto muy a su pesar, aboga por la desaparición de esta figura para facilitar el avance de la ciencia: primero por la tendencia existente en el resto de la comunidad médica a no contradecirlos, ya sea por deferencia, miedo o respeto; segundo, porque los editores de las revistas se enfrentan a la tentación de aceptar o rechazar nuevas ideas y evidencias en función de su coincidencia o no con la opinión «experta».
Esto no debe interpretarse como un rechazo a lo que uno puede aprender de sus maestros o colegas. Únicamente significa que, si se busca la mejor atención para nuestros enfermos, una «buena praxis» de la medicina moderna debe necesariamente partir de un conocimiento riguroso de las pruebas científicas que sustentan cada una de sus prácticas clínicas.
El «arte» de la medicina consistirá en saber combinar ese conocimiento con la valoración sopesada de si con ello se cumplen las expectativas de los pacientes, que son las que finalmente dan sentido a nuestras actuaciones.
LA PRÁCTICA DE LA MBE
Así pues, se trata de actuar en la clínica utilizando información seleccionada y relevante, y que venga avalada por datos obtenidos a través del método científico más riguroso: la epidemiología y la estadística. Ello no significa que haya que ser un entendido en epidemiología o en estadística para aplicar los principios de la MBE: es factible adquirir unas habilidades básicas que nos posibiliten tener juicio crítico para obtener la mejor evidencia científica del tema que nos interese [la mejor evidencia disponible, puesto que no en todos los campos existe evidencia de primera clase, sobre todo si la producción científica en el área de interés está dominada por las series de casos(13)].
La evidencia conseguida debe integrarse con la experiencia clínica individual y las expectativas, preferencias y deseos del paciente. Su práctica empieza y termina con el paciente.
La actividad clínica diaria genera cuestiones acerca de los efectos de la terapia, la utilidad de una prueba diagnóstica, el pronóstico de una enfermedad o la etiología de una determinada patología, lo que nos lleva a plantearnos una pregunta clínica (paso 1). A continuación realizaríamos una búsqueda bibliográfica (paso 2), evaluaríamos su validez y aplicabilidad (paso 3), y de nuevo volveríamos al paciente, integrando la evidencia con la experiencia clínica y sus preferencias (paso 4), evaluando el rendimiento de nuestra aplicación y cerrando el círculo de la MBE (tabla 1).

LA PREGUNTA CLÍNICA
Se pueden formular dos tipos de preguntas: las denominadas básicas constan de dos componentes y se plantean en relación al conocimiento general de un tema. Si me enfrento a un niño de 5 años con diagnóstico de retinoblastoma y habitualmente no trabajo con pacientes oncológicos, lo más probable es que me plantee una pregunta de dos componentes, (p. ej., tratamiento del retinoblastoma en un escolar), y para responderla podría acudir a un libro de texto clásico sobre oftalmología pediátrica. Sin embargo, la pregunta necesaria para la práctica de la MBE consta como mínimo de 3 elementos y se resume en los acrónimos PIO o PICO (Paciente, Intervención, Comparación, Resultado-Outcome en inglés), y no puede responderse recurriendo a un libro de texto, sino a artículos o revisiones sistemáticas. Este tipo de preguntas son las que se nos plantean en la práctica diaria en temas que sí conocemos y con los que trabajamos habitualmente. La C del acrónimo, la «comparación» no siempre es necesaria. Una pregunta clínica bien formulada va a facilitar enormemente la búsqueda de la evidencia al permitirnos traducir fácilmente nuestros términos a palabras clave (descriptores) (tabla 2).

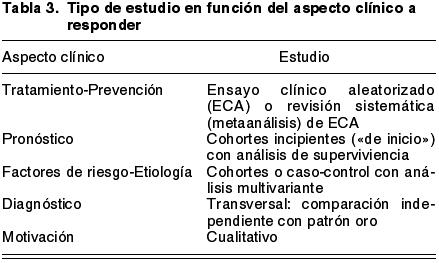
Una vez formulada la pregunta, debemos considerar qué aspecto clínico trata la pregunta: tratamiento o prevención, pronóstico, causalidad-etiología, elección de una prueba diagnóstica, riesgo-beneficio, calidad de vida, etc., y en función de esto sabremos qué tipo de estudio es el que mejor responde a la pregunta. En la tabla 3 se presentan los estudios adecuados en función de la pregunta a contestar. No debe confundirse la pirámide de la evidencia aportada por los distintos tipos de estudios (fig. 1) con la adecuación para responder preguntas clínicas. Así, es cierto que un metaanálisis de ensayos clínicos aleatorizados (ECA) aporta más evidencia que un ensayo clínico aislado, y éste a su vez es superior a un estudio de cohortes, y éste es superior a un caso-control, etc., pero un ECA no es el mejor estudio para valorar una prueba diagnóstica, donde no es necesario aleatorizar a los pacientes, sino realizar comparaciones independientes de la prueba a estudiar con la prueba de referencia (patrón oro); tampoco se presenta el ECA como el estudio a buscar en caso de factores de riesgo, puesto que es absurdo pensar en un ensayo clínico en el que los pacientes sean sometidos al azar a un posible factor de riesgo.
![]()
Fig. 1. La pirámide de la evidencia.
1 Estudio que mediante técnicas estadísticas combina los resultados
de varios estudios del mismo tipo (generalmente ensayos clínicos o estudios de
cohorte), obteniendo así un estudio con mayor muestra de población y, por tanto,
mayor potencia estadística.
2 Estudios centrados en una pregunta clínica concreta y elaborados a
partir de búsquedas extensivas de la literatura, seleccionando sólo aquellos
artículos metodológicamente correctos, cuyo contenido se evalúa y resume,
presentando una respuesta concreta a la pregunta clínica en cuestión.
LA BÚSQUEDA DE INFORMACIÓN
Las fuentes para responder a nuestra pregunta clínica son varias. Podemos recurrir a libros de texto tradicionales pero, como hemos visto, la información que contienen queda obsoleta con rapidez y no son adecuados para responder a preguntas de 3 componentes.
Se puede recurrir a bases de datos con filtro de calidad, como Embase, base de datos del repertorio Excerpta Medica; o la popular Medline (www.ncbi.nlm.nih.gov), base de datos del repertorio Index Medicus, producido por la National Library of Medicine y de libre acceso, a diferencia de Embase, gracias a la administración Clinton. Aunque en cualquier biblioteca podemos encontrar asesoramiento acerca de cómo realizar una búsqueda en Medline, en caso de no estar familiarizado con la mecánica se puede obtener un manual de trabajo en castellano a través de la página web www.fisterra.com, dedicada a atención primaria (http://www.fisterra.com/recursos_web/no_explor/pubmed.asp). En cualquier caso, la propia base de datos posee un buscador de preguntas clínicas (Clinical Queries) donde se pueden introducir los términos de búsqueda para terapia, diagnóstico, pronóstico o etiología, facilitando enormemente la realización de este tipo de búsquedas.
A partir de esta base de datos obtendríamos los artículos de interés, pero éstos deberán ser evaluados para valorar la evidencia que aportan. Una tercera alternativa es la búsqueda en revistas secundarias, que realizan el proceso evaluador por nosotros y nos ofrecen información ya revisada y catalogada desde el punto de vista de la evidencia a partir de artículos metodológicamente sólidos. Hoy en día existen en la red diferentes fuentes que proporcionan información de este tipo. En castellano se puede acceder a ellas a través de páginas como www.fisterra.com, o http://infodoctor.org, que contiene la página de Rafael Bravo, con múltiples recursos (http://infodoctor.org/rafabravo). La página web de la Universidad de Washington ofrece vínculos a distintas fuentes de MBE, incluyendo la colaboración Cochrane (http://healthlinks.washington.edu/ ebp/ebpresources.html).
Esta forma de utilización de la literatura médica en base a problemas clínicos constituye una medida más eficaz que la lectura tradicional para mantenerse al día y actualizar los conocimientos en la especialidad (14).
EVALUACIÓN CRÍTICA DE ARTÍCULOS RELACIONADOS CON EL TRATAMIENTO
Un artículo sobre tratamiento debe responder a 3 aspectos: validez de los resultados, importancia de los mismos y aplicabilidad a pacientes individuales. Analizamos y proporcionamos las herramientas para responder a estas preguntas: la evaluación de la validez interna, que garantiza que los resultados del estudio no están sesgados; el efecto del tratamiento y utilidad para nuestro trabajo diario.
La literatura médica ha de ser evaluada para valorar su nivel de evidencia, labor que realizan por nosotros las denominadas revistas secundarias, como el ACP Journal Club, la colaboración Cochrane o, más frecuentemente, nosotros mismos con la ayuda de las llamadas guías de lectura crítica. Esta labor de «evaluación», aunque pueda parecer farragosa en principio, nos permite, por un lado, conocer de forma rápida si merece la pena dedicar tiempo a un artículo y, por otro, limitar el número de artículos necesarios para mantenernos al día. Las guías de lectura crítica no son más que listas de verificación que deben cumplimentarse con los datos que obtenemos del estudio y que nos ayudarán a decidir sobre su idoneidad para responder a una pregunta clínica. En la tabla 4 se presenta la guía de lectura crítica que vamos a utilizar para los artículos sobre tratamiento.

Pueden obtenerse guías similares en las páginas web de la red CASP España, (Critical Apraissal Skills Programme) (15) o del centro para la medicina basada en la evidencia de la Universidad de Oxford (16).
¿En qué situaciones nos vamos a plantear la realización de una lectura crítica? Generalmente cuando queramos responder a una pregunta clínica determinada. Un ejemplo: en el último congreso de la Sociedad Española de Oftalmología, Vd. presencia una comunicación sobre la conveniencia de tratamiento de la hipertensión ocular mediante fármacos antihipertensivos, tras la que se establece cierta discusión. A la vuelta, y puesto que la discusión se estableció en base a una serie de casos, decide buscar si existe una evidencia más sólida. Vd. sabe que la máxima evidencia sobre la eficacia de un tratamiento se consigue mediante un ensayo clínico aleatorizado, y realiza una búsqueda bibliográfica a través de MEDLINE utilizando como palabras clave «ocular hypertension», «medical treatment» limitando la búsqueda utilizando como tipo de artículo la opción «randomized controlled trial». El resultado son 18 referencias bibliográficas entre las que se incluyen ensayos con distintos fármacos, comparaciones entre ellos y también un ensayo multicéntrico publicado en Archives of Ophthalmology (17), revista disponible en la biblioteca de su centro hospitalario.
LECTURA CRÍTICA ¿QUÉ DEBEMOS PEDIRLE A UN ARTÍCULO SOBRE TRATAMIENTO?
Las tres preguntas genéricas a las que debemos responder son:
1. ¿Son válidos los resultados del estudio?
2. ¿Cuál es la importancia clínica de los resultados?
3. ¿Son aplicables los resultados a mis pacientes?
En este artículo nos centraremos en responder la primera cuestión, es decir, en evaluar su validez, entendiendo como tal su validez interna, que garantiza que sus resultados no estén sesgados.
ANÁLISIS DE LA VALIDEZ
Identificación de la pregunta clínica
La identificación de los elementos de la pregunta clínica nos permitirá, además de evaluar su validez interna (ausencia de sesgo), conocer su aplicabilidad, es decir, la generalización de sus resultados a nuestros pacientes, en el caso de que la muestra utilizada sea representativa. En la tabla 5 se muestran los criterios de inclusión en el estudio elegido, las intervenciones a comparar y los resultados registrados, siendo el principal el desarrollo de un defecto en el campo visual o la afectación de la papila.

La importancia de la aleatorización
La segunda cuestión a responder, y posiblemente la más importante, es si el ensayo ha sido aleatorizado. Varias son las razones por las que es necesario que en un ensayo clínico exista una distribución aleatoria. La primera de ellas es que el muestreo aleatorio es imprescindible para que se cumplan los requisitos matemáticos de aplicación de los tests estadísticos. Toda la inferencia estadística y el cálculo de probabilidades se basan en el estudio de muestras extraídas al azar. La aleatorización es el único momento del diseño experimental en el que se introducen explícitamente las leyes del azar: ellas rigen la distribución de frecuencias teóricas que vamos a comparar con las frecuencias observadas. Así pues, sólo la aleatorización da sentido real al uso de los tests estadísticos [buscar la «p» o el intervalo de confianza (IC) al 95%], que se utilizan para medir el poder del azar en los resultados que se están encontrando.
La segunda es que la aleatorización de muestras grandes es el único método conocido de evitar el sesgo de confusión. Si en un experimento partimos inicialmente de dos muestras idénticas, y sobre una de ellas (pero no sobre la otra) realizamos una intervención, si al final aparecen diferencias entre ambas muestras podemos afirmar que la causa de las diferencias es la intervención. Si por el contrario, en un experimento partimos inicialmente de muestras que no son iguales, después de realizar la intervención sólo en una de ellas, si al final aparecen diferencias entre ellas no podremos achacar la causalidad de esas diferencias a la intervención. Así que la igualdad de las muestras es un requisito imprescindible para atribuir la causalidad, para concluir que la causa de las diferencias en el resultado final es la única variable distinta entre los grupos: la intervención que se está estudiando.
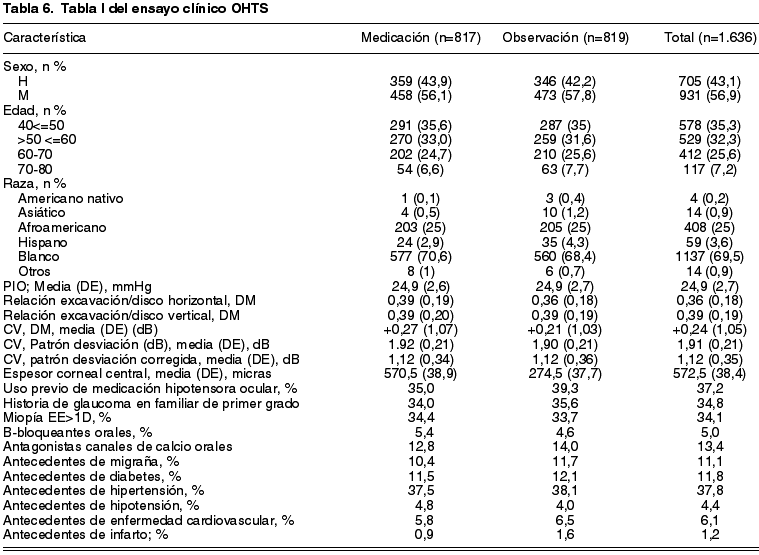
En base al teorema denominado la «Ley de grandes números» (LGN) (18), la aleatorización de muestras grandes tiende a producir grupos uniformes en todas las variables (incluidas las desconocidas), previamente a que se aplique la intervención en estudio. A consecuencia de esta ley, el control de las variables de confusión será proporcional al tamaño muestral: el teorema funciona si el muestreo es aleatorio cuando n (tamaño muestral) es . Como en nuestros ensayos clínicos nunca vamos a disponer de muestras infinitas, es imprescindible demostrar a los lectores de nuestros estudios que el efecto de la LGN para homogeneizar las muestras y controlar el efecto de los confusores principales se ha cumplido para el tamaño muestral que hemos elegido. Para ello sirven las llamadas «tabla I» de los trabajos: por consenso (19) se ha establecido que la primera tabla de un ensayo clínico debe mostrar la frecuencia de aparición de las principales variables demográficas y/o de confusión en ambas muestras antes de que se aplique la intervención. En esta tabla no encontraremos ninguna prueba estadística para comparar ambos grupos, ninguna p que nos diga que no existen diferencias estadísticamente significativas. La p no mide la homogeneidad, además de que una pequeña diferencia entre dos grupos alcanzaría significación estadística si el tamaño muestral fuera lo suficientemente grande. Es el lector el que, a la vista de los resultados y aplicando su juicio, evaluará si los grupos son comparables. En la tabla 6 se muestra la «tabla I» del ensayo que hemos elegido. Nótese el poder del azar para generar dos muestras muy similares, aunque no idénticas, como en el caso de los pacientes con antecedentes familiares de glaucoma o la asociación con miopía e hipertensión arterial, más numerosos en el grupo tratado con antihipertensivos tópicos. Usted, lector, tendrá que evaluar en base a sus conocimientos y experiencia si esa diferencia es significativa o puede influir en el resultado.
¿Cómo comprobar que se ha realizado una correcta aleatorización?
El término muestra aleatoria tiene una estricta acepción matemática que difiere del que se usa popularmente. En teoría, para que una muestra sea aleatoria se requiere que cada uno de los miembros de la población que se muestrea tenga la misma probabilidad de ser seleccionado para incluirse en la muestra: la probabilidad de asignación a los diferentes grupos es fija e igual para todos y cada uno de los individuos que participan. Este requerimiento no se cumple si la muestra se elige de manera fortuita (esto es, sin un plan específico) o de manera sistemática (números pares o impares de la historia clínica o días alternos de acudir a consulta) o conveniente (todos los que han devuelto un cuestionario contestado). Para obtener una muestra verdaderamente aleatoria de una población de pacientes se requieren maniobras especiales, como tirar una moneda insesgada, utilizar una tabla de números aleatorios o un generador computerizado de números aleatorios (20).
Como hemos visto, la aleatorización es la parte más sensible de todo el diseño. Por ello, para dar validez a los resultados del ensayo, deberemos aprender algunos «trucos» para detectar si la aleatorización ha sido realizada correctamente. El primero, que ya hemos citado, es comprobar que el azar ha generado muestras idénticas cotejando los datos de la llamada «tabla I». Pero quizá lo más curioso es saber que el muestreo aleatorio simple tiende a producir muestras homogéneas, pero de tamaños muestrales diferentes. La mayoría de la gente piensa que, por ejemplo, cuando distribuimos al azar en dos grupos (probabilidad de pertenencia a cada grupo= 0,5) un muestra total de 40 pacientes, cada una de las dos muestras resultantes deben poseer 20 pacientes. Nada más lejos de la realidad, pues la teoría de probabilidades nos permite calcular, utilizando la distribución binomial (fig. 2), que la probabilidad de obtener ese resultado es del 12,54%.
Es sorprendente encontrar en la literatura el enorme número de ensayos clínicos pequeños (menos de 100 pacientes) en los que el tamaño de los grupos que se comparan es igual cuando la muestra es un número par (30/30, probabilidad de presentación = 10,3%; 40/40, probabilidad = 8,9%) o hay un desequilibrio de uno cuando la muestra total es impar (17/16, probabilidad = 13,6%; 25/26, probabilidad 11%), cuando, sin embargo, dicen en los métodos que la distribución ha sido aleatoria. El hecho de que contradigan la teoría de probabilidades hace que estos trabajos sean sospechosos de que posiblemente no se ha realizado una aleatorización real, aunque sus autores así lo afirmen.
Es tan conocido entre los matemáticos que el muestreo aleatorio tiende a producir grupos de tamaños muestrales desiguales, que los estadísticos que trabajan con muestras pequeñas suelen utilizar muestreos especiales como el muestreo por bloques permutados balanceados. Por ello, un buen consejo para detectar que la aleatorización se ha realizado efectivamente es que, si se ha utilizado muestreo aleatorio simple, los grupos deben tener tamaño diferente. Si los grupos son iguales, se debe especificar en los métodos el sistema específico de aleatorización que se ha utilizado (p. ej., bloques balanceados).
En cualquier caso, ya hay pruebas empíricas (9) de que el factor que más sesga los resultados, sea cuál sea el método de aleatorización utilizado, es que no se respete la ocultación de la secuencia de aleatorización (OSA). La OSA (en inglés allocation concealment), un concepto diferente del enmascaramiento, consiste en que una vez ha entrado al estudio el primer paciente, debe ser imposible que el personal que administra la intervención adivine el grupo al que pertenecerá el próximo paciente que entre al estudio. Para que la aleatorización sea correcta debe asegurarse la OSA, y para ello los investigadores suelen utilizar varios métodos. El mejor es la aleatorización centralizada (vía telefónica o vía internet) en un centro coordinador diferente al resto de centros que aportan pacientes al ensayo, pero otros métodos válidos de OSA son la utilización de sobres opacos lacrados que contienen la intervención (o su etiqueta, si hay enmascaramiento, etc.) o, si se utiliza para la aleatorización el método de bloques balanceados, cambiar el tamaño de los bloques.
![]()
Fig. 2. Ley binomial de la probabilidad.
P(k): probabilidad de obtener k sujetos.
n: tamaño muestral total.
Una cuestión secundaria es el diseño ciego respecto al tratamiento. En un estudio ideal, tanto el paciente como el clínico, como el analista de los datos, desconocerían a qué grupo pertenece el paciente, pero esto no va a ser siempre posible. En el caso de terapias quirúrgicas frente a médicas es un buen ejemplo; o tratamiento médico frente a observación, como ocurre en el artículo que hemos seleccionado. En estos casos, al menos los autores habrán intentado que el analista de los resultados desconozca a qué grupo pertenecen los pacientes.
Seguimiento completo y análisis por intención de tratar
En segundo lugar, el seguimiento que se haya hecho de los pacientes deberá ser completo, es decir, que todo paciente reclutado para el estudio debe ser tenido en cuenta a su finalización, aunque en cualquier estudio van a existir pérdidas en el seguimiento. Si las pérdidas de seguimiento son excesivas, los resultados del estudio pueden ser puestos en duda, puesto que es frecuente que el pronóstico de los pacientes para los que no se dispone de seguimiento sea diferente al de los demás. ¿Cómo saber si las pérdidas de un estudio invalidan el resultado? Mediante el (worst case analysis). Consiste en suponer que todos los pacientes perdidos en el grupo control han evolucionado bien, y todos los perdidos en el grupo tratado han evolucionado mal, y volver a calcular los resultados. Si no se modifican los resultados del estudio, las pérdidas son asumibles. En caso contrario, la fuerza de los resultados se debilita en proporción a la probabilidad que existe de que los tratados hayan evolucionado bien y los del grupo control hayan evolucionado mal.
Aplicándolo a nuestro artículo, ambas ramas del estudio presentan 84 y 89 pérdidas de seguimiento a los 78 meses (fig. 3). Para el análisis de sensibilidad supondríamos que todos los perdidos en el grupo de tratamiento han desarrollado glaucoma y que los no tratados en el grupo control no lo han desarrollado. Parece que se modifican los resultados: el riesgo de desarrollar glaucoma en la rama de tratamiento se modifica (0,05 a 0,15%) y en la rama de observación se queda en 0,11%.

Fig. 3. Evolución de los pacientes reclutados en el ensayo
clínico.
Además de las pérdidas de seguimiento, es posible que los pacientes asignados en una u otra rama no tomen su tratamiento, no sea posible aplicarlo, o incluso que haya cambios de una rama a otra. En cualquier caso, el paciente será analizado dentro del grupo al que fue asignado independientemente del tratamiento que haya recibido. Es lo que se conoce como análisis por intención de tratar. Aunque en principio pueda parecer que si un paciente no ha recibido el tratamiento asignado debe ser excluido del análisis en esa rama, esto no es así. En muchos estudios, los pacientes que no toman la medicación evolucionan peor, aunque tomen placebo. En el caso de pacientes con patología quirúrgica, puede que algunos no lleguen a ser operados, puede que por gravedad. Si estos pacientes se incluyen en el brazo de control, incluso una operación inútil se mostrará como efectiva, ya que todos los pacientes con peor pronóstico se han asignado al grupo control (21).
Esta forma de análisis preserva el efecto de la aleatorización, y aproxima los resultados del estudio a la práctica clínica real. De hecho, en nuestro estudio de ejemplo 702 de los 817 pacientes aleatorizados al grupo de tratamiento tópico lo recibieron. En los 115 restantes no fue posible su aplicación, pero se analizaron igualmente en esa rama.
Igualdad de tratamiento al margen de la intervención
Ambos grupos de estudio deben recibir la misma atención. Si se realizara un seguimiento más estricto de una de las ramas podrían detectarse determinados hechos que no «aparecerían» en la otra rama, lo que podría afectar a los resultados.
Las intervenciones distintas al tratamiento en estudio, también denominadas cointervenciones, también pueden ser un problema (p. ej., utilización de beta-bloqueantes sistémicos como consecuencia de una cardiopatía isquémica), sobre todo si los facultativos conocen el tratamiento que están aplicando (no es un estudio a doble ciego) o se autoriza el uso de terapias muy eficaces, y distintas a las estudiadas, a criterio del médico (22).
¿ES VÁLIDO EL ARTÍCULO QUE HEMOS ELEGIDO?
Como hemos visto, el artículo define de forma concreta pacientes del estudio mediante criterios de inclusión bien definidos, define las alternativas terapéuticas que va a comparar, y el resultado que va a medir. De hecho, en la tabla 2 se presentan todas las variables que se recogen, aunque en el texto se define el evento primario como desarrollo de alteración en el campo visual o en las fotografías estereoscópicas de la papila, quedando los restantes como secundarios.
El estudio se define como aleatorizado. Nos informan de que utilizaron un análisis por intención de tratar y una secuencia de minimización para asegurar el equilibrio en las variables y un proceso de revisión en punto final para distinguir entre los cambios en el campo visual ocasionados por el glaucoma o los originados por otras causas. Se dispuso de central de aleatorización.
El tamaño de ambos grupos es creíble y vemos como el seguimiento fue casi completo, con 84 y 89 pérdidas por rama. El análisis fue por intención de tratar, manteniendo en la rama del tratamiento tópico aquellos casos en los que no se pudo aplicar. Por las características del estudio, fue doble ciego. Nos consta que el analista desconoce la pertenencia a las distintas ramas de tratamiento.
En definitiva, éste sí parece un artículo válido, por lo que seguiríamos con su lectura para responder a las dos siguientes cuestiones: efecto del tratamiento y utilidad para nuestro trabajo diario.
¿TIENEN IMPORTANCIA CLÍNICA LOS RESULTADOS?
La importancia de los resultados se determina mediante la magnitud del efecto y la precisión del mismo. No se va a utilizar pues la significación estadística. La «famosa» p en realidad nos está indicando la probabilidad de cometer un error tipo I o, lo que es lo mismo, afirmar que existen diferencias entre los tratamientos cuando no las hay y únicamente las hemos encontrado por azar. Si la muestra es de gran tamaño, diferencias de mínima magnitud pueden producir diferencias estadísticamente significativas. Debe remarcarse que la diferencia estadística no tiene por qué coincidir con la diferencia clínicamente relevante. Así, podríamos encontrar que una diferencia de 3 puntos en una escala de dolor de 0 a 100 fuera estadísticamente significativa, pero no tendría ninguna importancia en la clínica diaria.
Respecto a la magnitud del efecto, en el caso de variables continuas, como el tiempo de supervivencia o la puntuación en una escala de dolor, el resultado se expresaría como diferencia de medias o de medianas (pero recuerde que diferencia clínica y diferencia estadística no tienen por qué coincidir). Sin embargo, lo más habitual es que el estudio utilice variables binarias (afectación de campo visual sí/no, afectación de la papila sí/no, muerte sí/no, recidiva tumoral sí/no, etc.). En este caso la magnitud del efecto se expresa mediante el riesgo relativo (RR), la reducción del riesgo relativo (RRR), la reducción absoluta del riesgo (RAR) y el número de pacientes a tratar (NNT). Si el artículo no ofrece estos resultados, al menos debe proporcionar los datos necesarios para su cálculo.
En el artículo que estamos utilizando como ejemplo los autores no nos proporcionan estos valores, pero los hemos calculado a partir de la tabla 6. El evento registrado es el desarrollo de glaucoma primario de ángulo abierto a los 78 meses de seguimiento, por lo que un RR inferior a 1 nos indica que el tratamiento en estudio tiene un efecto protector.
El RR del tratamiento es 0,40 o, lo que es lo mismo, el riesgo de desarrollo de glaucoma en los tratados es 0,40 veces el de los no tratados. Esta medida se entiende más fácilmente si utilizamos la reducción del riesgo relativo (RRR): el riesgo de los tratados se reduce en un 60% respecto los controles. Si el RR fuera superior a 1 tendría un efecto perjudicial, ya que los tratados presentarían más probabilidad de desarrollo de glaucoma: un RR de 1,55 nos indicaría un riesgo superior en un 55% respecto al grupo control.
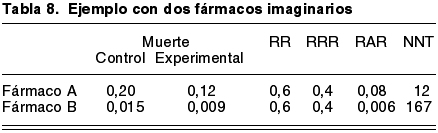
Ni el RR ni la RRR tienen en cuenta el riesgo basal de la población, cosa que sí hace la diferencia de riesgos o reducción absoluta del riesgo (RAR), que nos permitirá calcular el efecto de manera absoluta. La RAR tiene la particularidad de que es pequeña cuando los riesgos en los grupos son bajos, mientras que la reducción del riesgo relativo (RRR) permanece constante. Veamos un ejemplo: en la tabla 8 se muestran los resultados obtenidos con dos fármacos que se comparan contra placebo para curar una enfermedad. Se puede apreciar cómo ambos fármacos poseen el mismo RR y RRR, pero es la RAR (y en consecuencia el NNT) la que nos indica que el efecto del fármaco A es superior, ya que se aplica sobre una población con mayor riesgo basal. Esta peculiaridad es utilizada a menudo por la industria farmacéutica para promocionar sus productos, bien ofreciendo el RR o el RRR y ocultando la RAR si ésta es muy pequeña, bien ofreciendo las cifras que se obtienen en población con alto riesgo pero ofertando el producto también para población con bajo riesgo, donde el beneficio del tratamiento es a menudo desdeñable.

En cualquier caso, la mejor medida para expresar la eficacia clínica de una medida terapéutica es el NNT, o número de pacientes a tratar con el tratamiento experimental respecto a lo que hubiera pasado si recibieran el tratamiento control (placebo) para evitar un evento negativo (p. ej., desarrollo de glaucoma) o producir uno positivo (p. ej., curación). Y es la mejor medida porque exactamente eso es lo que necesita saber el clínico: cuántos pacientes ha de tratar con el nuevo tratamiento para curar a uno de ellos. En el caso de que se estudien efectos adversos se denomina número necesario para perjudicar (NNP): cuántos pacientes hay que tratar para producir un efecto indeseable. Como se muestra en la tabla 7, el NNT se obtiene a partir de la RAR.
En el estudio OHTS (17) por cada 16,66 pacientes tratados con antihipertensivos se evitaría un glaucoma primario de ángulo abierto, lo que significa que el tratamiento es tremendamente ineficaz en este grupo de población. Es importante no fijarse solamente en la RRR, sino también en la RAR. Con una RAR=25%, NNT es 4 mientras que con RAR=0,25% el NNT es 400: habría que tratar a 400 personas para evitar que 1 se convierta de HTO a glaucoma. El NNT disminuye conforme la PIO aumenta.
Además, también hay que tener en cuenta que la mayoría de tratamientos tienen efectos adversos que también se presentarán con cierta frecuencia. Para aquellos tratamientos con NNT elevados habrá que sopesar los posibles efectos adversos y el costo. Como norma general, ¡con NNT grande usar sólo si el tratamiento es barato, fácil e inocuo!
Lamentablemente, no podemos saber con certeza la reducción real del riesgo en los pacientes tratados. Los resultados obtenidos en la tabla 7 no son más que una estimación puntual del efecto real en la muestra seleccionada. Si tuviéramos a toda la población y no únicamente esta muestra, ¿el efecto sería el mismo? Para conocer la estimación real debemos calcular la precisión de nuestro resultado. Si es poco preciso es posible que el efecto estimado esté lejos del valor real. Esta precisión se cuantifica mediante el cálculo del intervalo de confianza (IC): podemos estimar un intervalo donde se encontrará el valor real en el 95% de los casos. Este 95% se acepta por consenso. Se puede trabajar con un intervalo de confianza del 90 o del 99%, pero cuanto mayor sea, mayor población será necesaria para estimar un intervalo de confianza estrecho.
Una vez obtenido el IC, habrá que observar si los resultados son estadísticamente significativos. Recuerde que para el RR el intervalo de confianza no debe incluir la unidad y para el NNT no debe incluir el 0. Si así fuera no podría sacarse ninguna conclusión útil del estudio, ya que no se habría demostrado diferencias entre ambos tratamientos. En caso de que el NNT no incluya el 0 (existen diferencias entre los tratamientos) habrá que observar los límites del intervalo y decidir, en función de su experiencia clínica, si le parecen asumibles. Un ejemplo: en el ensayo CAPRIE (23) de aspirina contra clopidogrel para prevención de eventos isquémicos cardiovasculares y cerebrales en población de riesgo un ensayo financiado por la industria farmacéutica aunque la reducción del riesgo relativo fue estadísticamente significativa (RRR 8,7%, p=0,043), el NNT fue de 197, con un IC 95% entre 84 y 1.001. Esto significa que es posible que se tuviera que tratar con clopidogrel a 1.000 pacientes para curar a uno más de los que se curarían usando aspirina. Si comparamos los precios de ambos fármacos (el clopidogrel es mucho más caro) no parece una decisión racional tratar a toda la población en riesgo de evento isquémico con el nuevo fármaco. El clopidogrel puede ser eficaz pero, con su precio, resulta extremadamente ineficiente.
Si el artículo no incluye el intervalo de confianza, éste puede obtenerse a través de la calculadora que ofrece la página web de la red CASPe (24) (una sencilla página de EXCEL), o mediante la fórmula que ofrece la guía de la universidad de Oxford (25):
IC95%RAR=RAR±1,96÷Rc(1-Rc)/Npacientes control + Re(1-Re)/N. pacientes expuestos
Con los límites superior e inferior del RAR se obtienen los límites superior e inferior del NNT
¿ME RESULTARÁN ÚTILES LOS RESULTADOS?
¿Pueden aplicarse estos resultados a mis pacientes?
Para responder a esta pregunta debemos plantearnos si nuestros pacientes, de haber estado en el estudio, hubieran sido incluidos en él, aunque quizá es más sencillo hacerlo al revés y preguntarnos si existe alguna razón por la que los resultados del estudio no sean aplicables a nuestros pacientes.
Una cuestión diferente es si su paciente se corresponde con un subgrupo de los incluidos en el estudio. ¿Qué hacer en ese caso? La primera cuestión es observar si los autores han realizado algún análisis de subgrupos, una situación relativamente frecuente cuando los resultados globales no muestran una clara superioridad del tratamiento en estudio y se intenta obtener mejores resultados en algún subgrupo. En muchas ocasiones estos análisis no estaban planificados al inicio del estudio, y sólo se recurre a ellos una vez obtenido el resultado global. Se pueden aceptar este tipo de análisis si se cumple alguno de los criterios de la tabla 9 (26).

¿Se tuvieron en cuenta todos los resultados clínicamente importantes?
Es importante que la variable resultado del estudio (end point) sea una variable clínicamente relevante cuya mejora justifique el uso del tratamiento. En el caso que nos ocupa se trata del desarrollo de glaucoma. Sin embargo, algunos estudios utilizan variables de valoración final indirectas (substituted end points) como podrían ser, disminución de PIO en 2-3 mmHg sin especificar el límite inferior (disminución de PIO <24 mmHg), diferencias en el anillo retiniano «escasamente detectables» o «clínicamente significativas». Que el tratamiento mejore esos parámetros no significa que sea necesariamente beneficioso para el paciente.
El estudio también debe considerar posibles efectos nocivos del tratamiento, que permitan sopesar el riesgo de seguir el tratamiento. En el estudio que nos ocupa se consideraron también como resultados secundarios el desarrollo de síntomas sistémicos u oculares secundarios al tratamiento utilizado.
¿Compensan los beneficios del tratamiento los posibles efectos adversos y los costes?
La respuesta a esta pregunta supone valorar globalmente los beneficios/perjuicios del tratamiento en nuestro paciente, junto con otras valoraciones que en principio pueden parecer más complejas, como el coste económico del tratamiento. En este apartado será de gran valor la experiencia personal para valorar cuestiones como la dificultad para aplicar el tratamiento, bien por motivos técnicos, bien por mala adherencia al mismo por parte del paciente, o por las dificultades logísticas que pueda suponer. Si valora la introducción de un nuevo colirio antihipertensivo tendría que valorar quién costearía el tratamiento, etc., una serie de cuestiones que sólo se pueden responder desde la experiencia y el conocimiento de las particularidades de cada caso.
CONCLUSIONES: HIPERTENSIÓN OCULAR Y TRATAMIENTO
Aunque en principio pueda parecer farragoso hemos visto cómo, a partir de los datos de un artículo válido y utilizando unas sencillas herramientas, es posible cuantificar el efecto de un tratamiento determinado y obtener conclusiones útiles para la clínica diaria. En nuestro caso, las conclusiones serían, en primer lugar, que no todos los individuos con PIO alta deben ser tratados. La decisión de instaurar tratamiento debe tener en cuenta muchos factores, como:
La baja incidencia de glaucoma primario de ángulo abierto entre los individuos con HTO en los diferentes estudios de base poblacional.
La conveniencia de un tratamiento a largo plazo: efectos adversos, coste.
El riesgo individual de desarrollar GPAA.
La probabilidad individual de beneficio por el tratamiento.
El estado general de salud del individuo y su esperanza de vida.
Ello justifica lo que ya nos suele indicar las revisiones Cochrane: se precisarán estudios aleatorios de mayor tamaño y con revisiones a largo plazo para establecer la pauta a seguir y conocer el tipo de beneficio que puede conseguirse para estos pacientes, antes de establecer las indicaciones definitivas de un tratamiento caro y no exento de complicaciones.
BIBLIOGRAFÍA
Sackett DL, Rosenberg WMC, Gray JA, Haynes RB, Richardson WS. Evidence based medicine: what it is and what it isnt. BMJ 1996; 312: 71-72.
Evidence-Based Medicine Working Group. A new approach to teaching the practice of medicine. JAMA 1992; 268: 2420-5.
Lopez Piñero JM, Terrada Ferrandis ML. Introducción a la medicina. 1.ª ed. Barcelona: Crítica 2000.
Cochrane Injuries Group Albumin Reviewers. Human albumin administration in critically ill patients: systematic review of randomised controlled trials. BMJ 1998;317:235-240. Disponible en internet en: http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pubmed&pubmedid=9677209.
López Piñero JM. Breve historia de la Medicina. 1.ª ed. Madrid: Alianza Editorial 2000.
Andrus CH. Ponsk JL. The effects of irrigant temperatura in upper gastrointestinal hemmorrhage: a requiem for iced saline lavage. Am J Gastroenterol 1987; 82: 1062-4.
Antman EM, Lau J, Kupelnick B, Mosteller F, Chalmers TC. A comparison of results of meta-analyses of randomized control trials and recommendations of clinical experts. Treatments for myocardial infarction. JAMA 1992; 268: 240-248.
Mulrow CD. Rationale for systematic reviews. BMJ 1994; 309: 597-599.
Davidoff F, Haynes B, Sackett D, Smith R. Evidence based medicine: a new journal to help doctors identify the information they need. BMJ 1995; 310: 1085-6.
Bodenheimer T. The American health care system -the movement for improved quality in health care. N Engl J Med 1999; 340: 488-492.
Feynman RP. En busca de nuevas leyes (Messenger Lectures de la Cornell University, 1964). En: Museu de la Ciencia de la Fundación «La Caixa», editor. El carácter de la Ley Física. Barcelona: Tusquets Editores 2000; 165-190.
Sackett DL. The sins of expertness and a proposal for redemption. BMJ 2000; 320: 1283.
Weil RJ. The future of surgical research. PLoS Med 2004;1:e13. Disponible en internet en www.plosmedicine.org.
Shin JH, Haynes RB, Johnston ME. Effect of problem-based, selfdirected undergraduate education on life-long learning. Canadian Medical Association Journal 1993; 148: 969-976.
http://www.redcaspe.org/herramientas/lectura/ 11ensayo. pdf.
http://www.cebm.net/worksheet_therapy.asp.
Kass M, Heuer D, Higginbotham E, Johnson C, Keltner J, Miller P, Parrish R, Wilson M, Gordon M. The Ocular Hypertension Treatment Study: a randomized trial determines that topical ocular hypotensive medication delays or prevents the onset of primary open-angle glaucoma. Arch Ophthalmol 2002; 120: 701-708.
Rice JA (1995). Limit Theorems: The law of large numbers. En: Mathematical statistics and data analysis. 2.ª Edición. California. Duxburi Press.
Begg C, Cho M, Eastwood S, Horton R, Moher D, Olkin I, et al. Improving the quality of reporting of randomized controlled trials: The CONSORT statement. JAMA 1996; 276: 637-639.
Feinstein AR (2002) Principles of medical statistics. 1.ª Edición. Florida. Chapman&Hall/CRC.
Egger M, Ebrahim S, Smith GD. Where now for meta-analysis? Int J Epidemiol 2002; 31: 1-5.
Guyatt GH, Sackett DL, Cook DJ. Guías para usuarios de la literatura médica II. Cómo utilizar un artículo sobre tratamiento o prevención. A. ¿Son válidos los resultados del estudio? JAMA 1993; 270: 2598-2601.
CAPRIE steering comitee. A randomised, blinded, trial of clopidogrel versus aspirin in patients at risk of ischaemic events. Lancet 1996; 348: 1329-39.
http://www.redcaspe.org/herramientas/descargas/tratamientos.xls
http://www.cebm.net/worksheet_therapy.asp.
Guyatt GH, Sackett DL, Cook DJ. Guías para usuarios de la literatura médica. II Cómo utilizar un artículo sobre tratamiento o prevención. JAMA 1994;271:59-63.